How To Set Up A Proportion
Proportions
A ratio is one thing or value compared with or related to another thing or value; it is just a argument or an expression, and can only perhaps be simplified or reduced.
On the other paw, a proportion is two ratios which have been set equal to each other; a proportion is an equation that can be solved.
When I say that a proportion is two ratios that are equal to each other, I hateful this in the sense of two fractions beingness equal to each other. For example, equals .
Content Continues Below
Solving a proportion means that we accept been given an equation containing two fractions which take been prepare equal to each other, and we are missing i part of one of the fractions; we and then need to solve for that one missing value. For instance, suppose we are given the following equation:
We already know, by just looking at this equation and comparing the two fractions, that 10 must be equal to 5, but let's suppose for the moment that we hadn't noticed this. We tin can solve the given equation past multiplying through on both sides by 10 (or, if one prefers, ) to clear the denominators:
Verifying what we already knew, we become a solution of x = v.
Often times, students are asked to solve proportions earlier they've learned how to solve rational equations, which can exist a fleck of a problem. If ane hasn't nevertheless learned near rational expressions (that is, polynomial fractions), so information technology will be necessary to "go by" with "cross-multiplication".
To cross-multiply, nosotros start with an equation in which two fractions are set equal to each other. Then nosotros have each denominator and move it across the "equals" sign and and then MULTIPLY it against the other fraction'south numerator. The cross-multiplication solution of the above exercise looks like this:
Then nosotros would solve the resulting linear equation past dividing through by 2 to again get in at x = 5.
Note the process in the above. Nosotros multiplied the left-hand side's denominator by the right-manus side's numerator, so divided by the right-hand side'due south denominator. You may run into this process explicitly applied for the solving of proportions. The method of solution would then by to cross-multiply the numbers (that is, in the direction that does not involve the variable), and then divide by the remaining number. In very informal note, the process looks like this:
![]()
The green arrow pointing northeast (that is, from bottom left to upper right) indicates the multiplication footstep; the majestic looping arrow that ends up pointing at the variable indicates the division step.
-
Solve the proportion:
The variable in this proportion is in the denominator of the correct-hand side'southward fraction, but that'south okay. I can still cantankerous-multiply and solve.
The solution of the proportion is the value of the variable, and so my respond is:
y = 39
If I'd done the autograph method (shown with the green and regal arrows higher up), the computations would accept been:
(13 × 18) ÷ vi = 39 = y
It'due south harder to "show your piece of work" using the shorthand method, but the shorthand method is easier to plug into your figurer. Utilize whatever method works well for you.
-
Solve the proportion:
I'll cross-multiply, and so separate:
Hm... Can proportions have fractional solutions? Yes, definitely; they can! I mustn't let the only-whole-number exercises and examples mislead me into thinking that proportions must always accept whole-number answers. They don't. My fractional answer is perfectly fine.
Proportions wouldn't be of much utilise if you lot merely used them for reducing fractions. A more than typical employ would exist something like the post-obit:
-
The ratio of waterfowl in a given park is xvi ducks to 9 geese. Suppose that there are 192 ducks in total. How many geese are there in total?
They've asked me to solve for an unknown value, so I'll demand an equation with a variable. They've given me a ratio, so my equation will be a proportion.
I'll permit " Thou " stand for the unknown number of geese. I'll clearly characterization the orientation of my ratios (then I don't misfile which number stands for what), and then I'll ready my proportional equation:
![]()
I'll cross-multiply to solve for the value of Thousand:
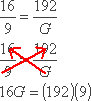
16G = 1728
Thou = 108
I labelled things clearly at the commencement, and then I know that " G " stands for "the number of geese in the park". So my respond is:
108 geese
"Cross-multiplying" is standard classroom language, in that it is very commonly used past students and instructors, just it is not technically a mathematical term. You might not see "cantankerous-multiplication" mentioned in your textbook, but you will almost certainly hear it in your grade or study group.
Notice how, when I was setting up my equation at the beginning of my solution to a higher place, I prefaced my proportion by writing out my ratio in words; namely:
![]()
This is not standard notation (in the sense of your textbook beingness likely to use it), but it tin be very helpful for setting up proportions. Past clearly labelling which values are represented by the numerators and denominators, respectively, you volition help yourself go along runway of what each number stands for; you won't mix upwardly which number or unit of measurement goes where.
In other words, using this method will help y'all set up up your proportions correctly. If you practice not set up the ratios consistently (for case, if, in the higher up example, I'd mixed up where the values for the "ducks" and the "geese" were supposed to get in the various fractions), I'd have gotten an incorrect answer. Clarity in your set-up is crucially important when working with proportions. Nosotros will return to this subject afterwards.
Source: https://www.purplemath.com/modules/ratio2.htm

0 Response to "How To Set Up A Proportion"
Post a Comment